The usefulness of sin() and cos()

    In my last post we stereo-typically used trigonometric functions to calculate an angle. It's important to note that although this is the primary use for said functions, the range of values of said functions, primarily sin() and cos(), have a wide variety of uses in game development, which we will explore below. We'll start by analyzing the properties, we'll talk about a situation where they can be used efficiently, and finally show an unreal engine example.

    As with all functions, understanding the domain and range of sin() and cos() is of great importance. As I'm not trying to re-create a trigonometry class, I will avoid going into too specific of details:

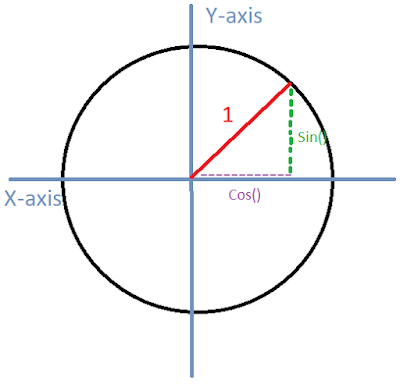
(Figure 1: Unit Circle Model)

1 - Range: The values we get when we plug values of the domain into a function. For sin() and cos(), imagine at the center of the circle in figure 1 we have our player, and as in my previous post we're trying to calculate an angle about the Z-axis. The direction we wish to face is represented by the line labeled 1. Due to the concept of similar triangles we can create a circle with radius 1, which allows us to prove that sin() corresponds to the y axis portion of our angle and cos() represents the x portion using SOHCAHTOA. Therefore, as we increase our angle, or turn about the origin in a counterclockwise direction, we find that the range of values for sin() and cos() are -1 to 1, including the -1 and 1. 

2 - Domain: The values we can plug into a function. As we rotate about the origin, a.k.a increase our angle, we notice at some point, 360 degrees to be exact, we end up at the same angle. We can continue rotating in EITHER a clockwise or counter-clockwise in 360 degree chunks and also end up at the same angle. Therefore, for angles between 0 and 360 and their subsequent, equivalent angles, since there are no values in which sin() and / or cos() are undefined, both sin() and cos() can have any real number (number with or without a decimal) plugged into them.

    In short, sin() and cos() spit out values between and including -1 to 1 for any value we give them.

(Figure 2: Graph of Sin() )

    So how does that help us? Well, if we were to plot all the values of sin() we'd get the approximated graph shown in figure 2. As we can see, we get this interesting back and forth pattern, which can be used for all types of sweeping, back-and-forth movement scenarios. NOTE: cos()'s graph is nearly identical to sin()'s graph, except it's shifted to the left so that cos() of 0 is 1, whereas sin() starts at 0.

   Lets assume we're making a power-up, and we want to bob it up and down, just to give it a bit of life from the rest of the world around it. We could simulate this effect with a variety of variables and a series of if statements, or we can apply one variable and a trig function to accomplish the same task.

(Figure 3: code snippet of power-up bobbing motion)

    Figure 3 showcases just how easy it is to apply a bobbing motion to an object / actor. we start creating a variable, in this case called animAngle. This variable will hold the ever increasing angle that will be plugged into the sin() function. The smaller the angle is incremented every frame, the smoother the movement. In this instance, we'll use the value of 'delta_time', which is, without getting too technical, the closest measurement of real time passage between game frames. We simply take the sin() of this animAngle, which is incremented at the end of the event tick() event chain, and add this movement to the axis of choice, in this case the Z-axis.

   In figure 3 I use the delta seconds float tied to the event tick() event to get the delta time. If you don't have access to the event tick() event you can use the "Get World Delta Seconds" blueprint to grab the same value.

   This is only part of the magic. Left as it is, you'll probably find it bobs up and down too high and too slowly, surely there's a way to rectify this, and sure enough, there is: We need to affect the amplitude and period of the function.

   ...Forgive the fancy words. Simply put, with a multiplication / division here and there, we'll be good as gold, maybe better.

(Figure 4: Partial Trigonometric Formula Including Amplitude (A) and Period (B) Only)

1 - Amplitude: Also considered the magnitude, this value affects the distance away from the starting position the object / actor will travel back and forth, also referred to as oscillation. By multiplying the result of the trigonometric function, in this case sin(), by a number larger than 1, we increase the travel distance, while multiplying by a fraction will yield a smaller distance traveled.

2 - Period: Over the course of an ever increasing 'x' value, the value of a trigonometric function resets and repeats itself. This is known as the period. By multiplying the angle before it gets plugged into a trigonometric function, we can increase / decrease the speed at which the oscillation occurs. Multiplying by a number greater than 1 will speed up the oscillation speed, and if 'B' is a fraction it will slow down the period.

   It is worth noting that affecting the period will affect the amplitude, as it reduces the number of times the amplitude can affect the values of the trigonometric function, so if you adjust the period you may need to re-adjust the amplitude to compensate one way or the other.